RiemanLine: Riemannian Manifold Representation of 3D Lines for Factor Graph Optimization
Abstract:
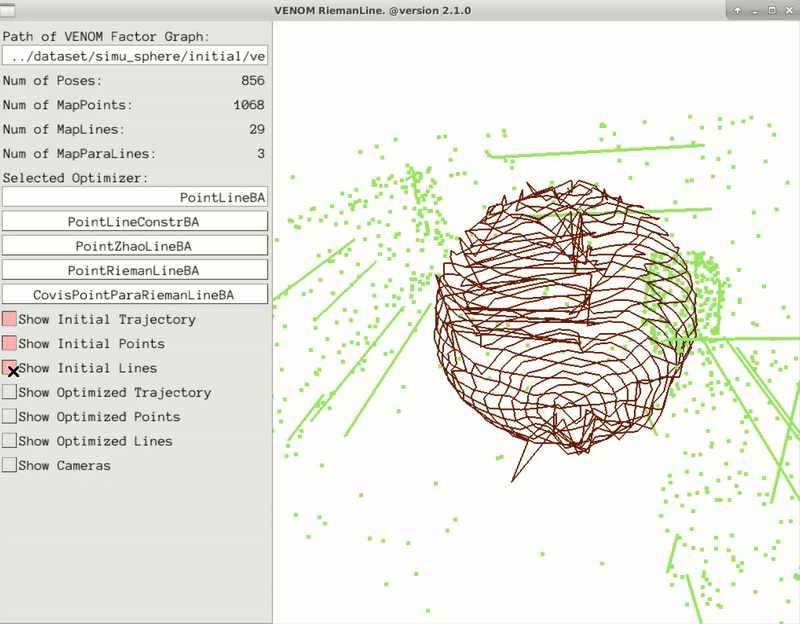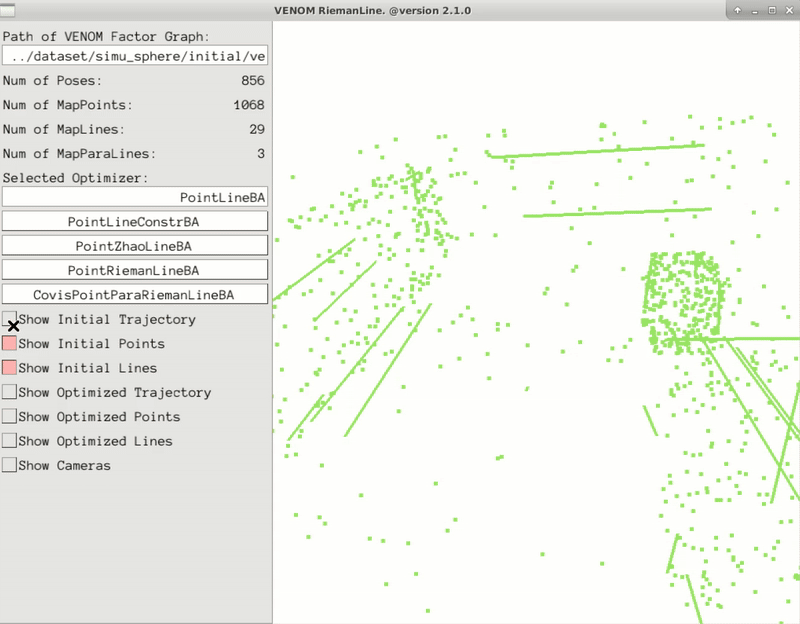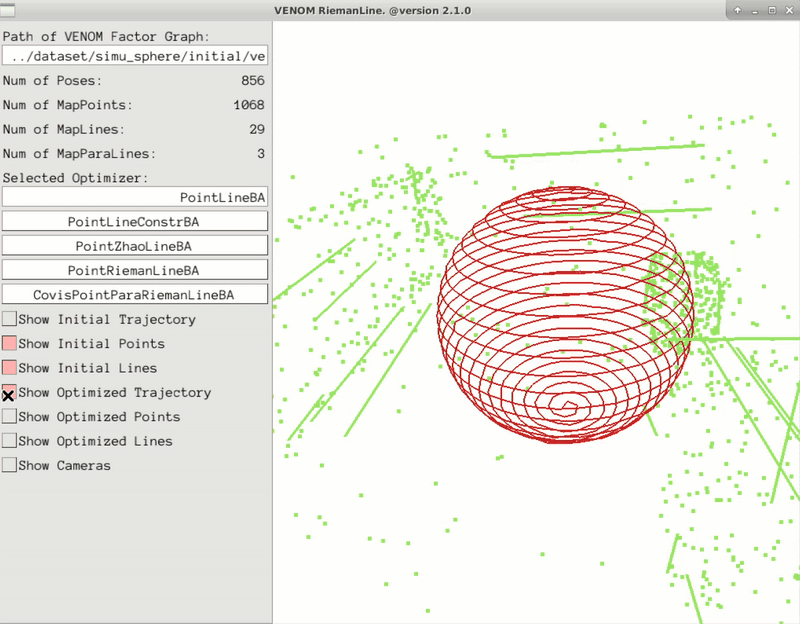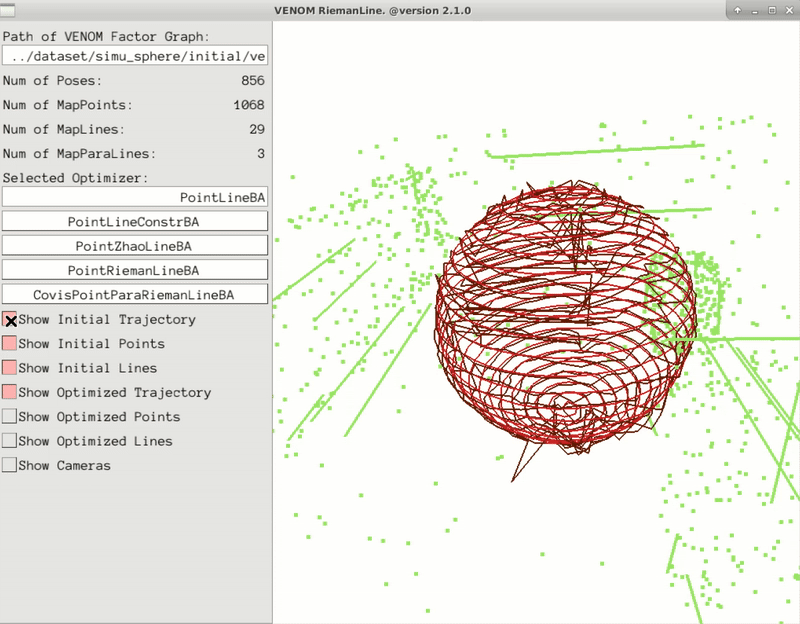
Minimal parametrization of 3D lines plays a critical role in camera localization and structural mapping. Existing representations in robotics and computer vision predominantly handle independent lines, overlooking structural regularities such as sets of parallel lines that are pervasive in man-made environments. This paper introduces RiemanLine, a unified minimal representation for 3D lines formulated on Riemannian manifolds that jointly accommodates both individual lines and parallel-line groups. Our key idea is to decouple each line landmark into global and local components: a shared vanishing direction optimized on the unit sphere, and scaled normal vectors constrained on orthogonal subspaces, enabling compact encoding of structural regularities. Extensive experiments on ICL-NUIM, TartanAir, and synthetic benchmarks demonstrate that our method achieves significantly more accurate pose estimation and line reconstruction, while reducing parameter dimensionality and improving convergence stability.